Тема №22: Числові послідовності
Тема уроку. Арифметична
прогресія. Розв’язування задач
Мета уроку: 1). Узагальнити знання
учнів з теми «Арифметична прогресія»; закріпити поняття послідовності, навички
обчислення елементів прогресії; провести зрізи знань з метою встановлення рівня
усвідомлення навчального матеріалу; показати зв’язок алгебри з життям і побутом,
практичне застосування теми на прикладах історичних задач; удосконалити роботу
в групах.
2). Розвивати логічне мислення,
творчу та розумову діяльність, вміння аналізувати та чітко і зрозуміло
висловлювати власну думку; вміння самостійно здобувати знання, використовуючи
різні інформаційні технології та оцінювати свої досягнення.
3). Виховувати інтерес до предмету, культуру записів, увагу та взаємодопомогу,
працьовитість та працездатність.
Тип уроку: урок узагальнення і
систематизації знань.
Обладнання: роздавальний матеріал,
підручник, проектор.
Хід урок.
Прогрес – це рух, це велич, це зростання,
Як Україні зараз він потрібний,
Прогресії – його сестриці рідні.
Це школа, математика, навчання.
І кожен з нас, як аксіому знає:
Без математики на ноги нам не стати,
Тож хай лунає лозунг наш крилатий:
«Прогресу без прогресій не буває!»
І. Організаційний момент (0,5хв.)
ІІ. Перевірка виконання
домашнього завдання. (1хв.)
Чергові учні до початку
уроку перевіряють підготовку учнів до уроку (наявність розв’язаних вправ), на
протязі уроку вчитель дає відповіді на запитання, які виникли у школярів під
час виконання домашньої роботи.
ІІІ.
Мотивація навчальної діяльності (1хв)
«Перша умова, якої треба дотримуватися в
математиці, – це бути точним. Друга
– бути чітким, і наскільки можливо, простим».
(Л. Карно)
Отже, ми сьогодні з вами на уроці просто, чітко і з легкістю узагальнимо знання з теми: « Числові
послідовності. Арифметична прогресія», закріпимо поняття послідовності та навички
обчислення елементів прогресії, покажемо зв’язок математики з життям і побутом
та розглянемо практичне застосування теми на різних задачах, будемо
удосконалювати вміння оцінювати свої досягнення.
ІV. Активізація і актуалізація опорних знань учнів. (до 18 хв)
«Знання збираються по краплині, як вода в долині».
1). Дев’ятикласникам,
заздалегідь, було запропоновано самостійно об’єднатися у три групи і
підготувати презентації - відповіді на низку запитань за вивченими темами: І-й
групі - тема « Числові послідовності.», ІІ - й групі - «Арифметична прогресія »,
ІІІ – й – « Прогресія в житті та побуті ».
Презентація І групи (2-3хв) Числові послідовності
Учні демонструють свою роботу і відповідають по черзі,
на питання, що їм поставили представники іншої групи. Команди повинні
відповідати швидко і чітко на поставлені запитання, використовуючи слайди.
Запитання
для учнів І групи – «Числові послідовності»
1. Наведіть приклади
числових послідовностей.
2. Сформулюйте означення
числової послідовності.
3. Якими бувають числові
послідовності?
4. Які послідовності
називають скінченими?
5. Які послідовності
називають зростаючими? А які - спадними?
6. Назвіть п’ять перших
членів послідовності: а) парних чисел; б) непарних чисел.
2). Колективна робота з класом
Усні вправи ( до 4хв)
1.
Дано скінченну послідовність: (хп): 3; 0; -3; -6; -9; -12.
Укажіть:
1) перший, третій, шостий члени цієї послідовності;
2) чи є ця послідовність
зростаючою, спадною;
2.
Послідовність (ап)
задана формулою ап = 3п
– 1. Укажіть:
1) а1, а2,
а3;
2) номер
члена, який
дорівнює 26;
3) чи є членом цієї послідовності число 47; 58?
3. Робота з підручником №886(а, б), №
867(а)
Під час короткої презентації і роботи класу з усними
завданнями, 5 учнів класу одержують картки ( з диференційованими завданнями) для
перевірки знань: І варіант №1-3, ІІ варіант №4-6 (з подальшою самоперевіркою).
Робота з картками (5-6 хв )
3). Презентація ІІ групи (2-3хв). Арифметична прогресія
Запитання
для учнів ІІ групи - «Арифметична прогресія»
1. Сформулюйте
правило означення арифметичної прогресії.
2. Чому
прогресія називається арифметичною?
3.
Що
таке d?
4.
Як
знайти d?
5.
За
якою формулою знаходять будь-який член арифметичної
прогресії?
прогресії?
6.
Що
означає формула аn =
аn-1 +
d?
7.
Як
знайти суму членів арифметичної прогресії?
8.
Коли
прогресія є зростаючою?
9.
Коли
прогресія спадна?
10.Сформулюйте властивість арифметичної прогресії.
Після короткого повторення учням класу
роздають завдання
для перевірки своїх знань І варіант №1-3, ІІ варіант №4-6 ( з різними рівнями
складності) ( з подальшою перевіркою) ( до 7хв)
Учитель
проводить підсумок цього етапу уроку.
V. Закріплення і
засвоєння теоретичного матеріалу. (15 хв.)
1). (Робота з підручником Г.П. Бевз, В.Г. Бевз,
2009 « Зодіак - ЕКО», 2009)
а). Робота біля дошки № 914,
б).
Робота в групах ( в парах) №888 ( стародавня арабська задача)
2). Презентація цікавих задач
3). Презентація роботи ІІІ групи (5
хв). Прогресія в житті та побуті
VІ. Підведення
підсумків уроку. (2хв)
1).Отже,
на сьогоднішньому уроці ми узагальнили і систематизували знання з теми
арифметична прогресія, закріпили
навички обчислення елементів прогресії , працювали з картками, вияснили
роль прогресії у життя і побуті, розглянули стародавню арабську задачу.
2).
Виставлення оцінок.
VІІ.
Домашнє завдання. (3хв)
Опрацювати §20, 21; №№ 889, 882(а),
№899 (а) – для всього класу
1). Завдання для ІІІ групи: «Спробуйте
у свій вільний час розшукати відповіді на питання:
а). Яка відома історія трапилась із Карлом
Гаусом у 7 років?
б). Послухайте легенду: «Індійський цар Шерам покликав до
себе винахідника шахової гри, свого підданого Сету, щоб нагородити його за
дотепну вигадку. Сета, знущаючись над царем, попросив за першу клітку шахівниці
- 1 пшеничне зерно, за другу – 2, за третю – 4 зернинки і т.д. Як виявилось,
цар не зміг задовольнити це «скромне бажання Сети»». Чому це трапилось?
Знайшовши відповіді на ці питання ви допоможете мені
пояснити новий матеріал на наступному уроці.
2). Завдання для ІІ групи: № * Розв’язати завдання (
підготовка до ЗНО)
Знайти
корені рівняння 1 + 7 + 13 + …. + х = 280, х
.
Розв’язання.
Ці числа утворюють арифметичну прогресію, в якій
Використавши формулу
n-го члена арифметичної прогресії
, знайдемо, що
. Використавши формулу
, маємо рівняння
. Звідки х = 55 або х = -61. Оскільки за умовою задачі х
, то х = 55.
Відповідь:
55.
3). Завдання для І групи – «Скласти кросворд».
1. Послідовність, кожний член якої,
починаючи з другого, дорівнює попередньому члену, до якого додано одне й те
саме число.
2. Спосіб задання послідовності.
3. Будь – яке число в арифметичній
прогресії.
4. Число d.
5. Натуральне число, яке означає місце
члена в послідовності.
6 аn= a1 + d (n – 1)
Використана література
1.
Програма для загальноосвітніх навчальних закладів. Математика 5-12 класи. – К.: Перун Ірпінь,
2005.
2.
Бевз Г. П. Алгебра-9. Підручник для 9 класу. –
Київ: « Зодіак – ЕКО», 2009.
3.
Дубинчук О.С., Мальований Ю.І., Дичек Н.П. Методика викладання алгебри
в 7 – 9 класах. Посібник для вчителя. Київ: « Радянська школа».
4.
Глейзер
Г. И. История математики в школе.- Москва: Просвещение, 1982.
5.
Крамор В.
С. Повторяем и систематизируем школьный курс алгебры и начал анализа. Москва:
Просвещение, 1990.
6.
Вишенський В. А. Посібник-довідник для вступників
до вищих навчальних закладів. – Київ: Генеза, 1993.
7.
Журнал “Математика в школі”, №6, 2004. – С. 19-20.
8.
Журнал “Математика в школі”, №6, 2007. – С. 19-22.
9.
Журнал “Математика в школі”, №5, 2008. – С. 20-22.
10.Журнал “Математика в школі”, №2, 2009. – С. 9-13.
Корисно відвідати
nhttp://www.mon.gov.ua/ - офіційний сайт Міністерства освіти та
науки України.
nhttp://www.iteach.com.ua –
український сайт програми Intel «Навчання для майбутнього».
nhttp://www.iteach.ru — російський сайт програми Intel «Навчання
для майбутнього»
nhttp://www.intel.com/education/teach - Intel® Teach

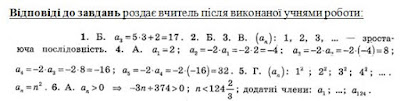




Комментариев нет:
Отправить комментарий